Nx Sharding Update - Part 1

Whether you need end-to-end product development support or the engineering know-how for a targeted project, we can help. Book a free consult to learn more.

This blog post is the start of a series in which I’ll be providing updates on the development of data sharding in Nx.

Up until now, Nx has had the ability to compile defn functions into efficient native code. This code also has the ability to run concurrent requests throughout a cluster via the Nx.Serving module. However, these requests have always been executed in a single process, and therefore without any distribution capabilities in the execution itself, unless the user manually handled the function splitting and the processing distribution.

Sharding changes this, because it allows Nx to split and distribute the input data and the computation itself among multiple processes and potentially multiple BEAM nodes.

What is Sharding?

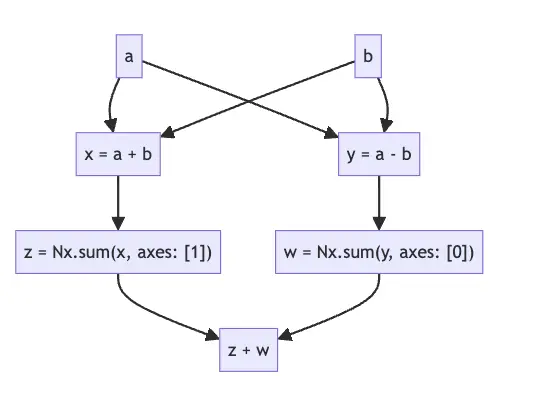
To explain sharding, we need to take a step back and analyze how Nx understands defn functions. Let’s start with the example below:

defn f(a, b) do
  x = a + b
  y = a - b
  z = Nx.sum(x, axes: [1])
  w = Nx.sum(y, axes: [0])

  z + w
end

This defn function is parsed by Nx into a data structure called Nx.Defn.Expr. This is the equivalent of an Abstract Syntax Tree (AST) in Nx, and can be modeled by the diagram below:

This means that we now have a symbolic representation that can be manipulated and analyzed as needed.

Now let’s look at x and y. Each one is created by an element-wise binary operation, which means that their points can be calculated independently from each other. This independence indicates that if we split the input data and manipulate our Nx.Defn.Expr in a special way, we might be able to calculate things in parallel.

This act of splitting the input data and then propagating this separation through the computation graph is what we call Data-Level Computation Sharding, or Sharding for short.

Achieving Data Sharding in Nx

The proposed Sharding implementation consists of annotating how the inputs are split, and then propagating this information through the Nx.Defn.Expr graph.

If we take a to be a 10x8 tensor, we can have an annotation that is similar to the following:

%{
  0 => [
    %Shard{id: 0, range: 0..4, parents: []},
    %Shard{id: 1, range: 5..9, parents: []}
  ],
  1 => [
    %Shard{id: 2, range: 0..3, parents: []}
    %Shard{id: 3, range: 4..7, parents: []}
  ]
}

This can be visualized as the animation below, where we’re splitting our data into 4 distinct Data Sections. Note that the ids for each data section are composed by the ids of the shards that make up the section, ordered by axis.

The Data Sections themselves aren’t really important in the forward pass, and we only care about the axis-wise sharding. Note that each shard has its own id (represented in Elixir by a unique Ref) and it can have parents.

Some similar annotation could be made into b as well, but we can assume that if none is given, all data is independent until proven otherwise - that is, b is Fully Sharded a priori.

Now, how do we calculate x = a + b? The implementation details aren’t as important here as the concepts, so we’ll stick to the conceptual analysis. Each operation should define a shard propagation rule, in which it decides how its output is sharded based on the input or inputs.

For element-wise binary operations, such as addition, the rule goes as follows:

• If one of the operands is Sharded and the other is Fully Sharded in a given axis, child shards are created such that they take the same values as the Sharded operand, with a new id, and the parents are the immediate shards that are involved in the operation. This is the case described above for a and b.
• If both operands are Sharded and the sharding is compatible (for example, the same number of shards on that axis), we can apply the same process of creating a new Shard with parent Shards.
• Otherwise, we have a sharding conflict and the compilation must halt.

There are some details that pertain to implicit operand broadcasting (for example if we have a scalar + matrix situation), but these won’t be discussed here.

The animation below shows the Sharded + Fully Sharded case along the columns and the compatible sharding case along the rows.

As we propagate these shards forward, we will at some point arrive at the output node. From there, we can take each output Data Section (for instance, the one specified by Shard 0 and Shard 2, or Shard 0 and Shard 3 – see the first animation for a visual representation of this) and trace the parent shards until we reach the required data sections in the inputs.

The inputs can then be sliced with Nx.slice and passed to the function. The result for each instance will now be calculated with this reduced dataset, and then we can put everything together with Nx.put_slice or some equivalent tensor construction function.

The Problem with Nx.sum

Until now, we avoided discussing how Nx.sum plays into sharding. Nx.sum is what we call a reduction operation because its results require an axis-wide calculation. This means that for calculating z = Nx.sum(x, axes: [1]), we would need x to be at best, divided in such a way that rows aren’t split at all. This would mean that the shards with ids 2 and 3 above can’t exist.

Does this mean that we must invalidate that configuration implicitly or fail the compilation altogether? Fortunately, no. In the next installment in this series, we will have an in-depth discussion on the Graph Splitting compiler pass. However, before we sign off, we can at least describe at a higher level how it works in tandem with the Shard Propagation:

• Shard Propagation will eliminate sharding on reduction axes. This means that these shards won’t appear in the output, and when we trace the output shards back to the input, we will require the full axis instead.
• Graph Splitting can then traverse the expression, creating splits at each reduction operation, in such a way that the computation becomes a series of execution Stages. This means that a previous Stage can still take advantage of sharding, even if the data has to be gathered together for the next Stage.

Next Steps

In the next installment, we will discuss Graph Splitting in depth, and start thinking about how we can connect everything together to leverage the full power of BEAM distribution.